
I’m no machine learning engineer
Duh. I’ve spent long enough reading about and experimenting with machine learning now that I guess I understand the basics more than most, but obviously I have no formal training or professional experience, so obviously take everything I have to say here with massive, Milton-sized grains of salt.

Since getting access to ChatGPT, I find I can learn about ML way, way faster though, and I’m really enjoying it.
I was watching this interview with OpenAI chief scientist and machine-learning legend Ilya Sustkever and at one point he and Lex Fridman discuss the phenomenon of double descent. What the heck is that?
A really, really basic explanation of machine-learning and stochastic gradient descent
Essentially, as I understand it, one of the fundamental ideas behind deep-learning (the subset of machine-learning driving pretty much all of the AI revolution in the past number of years) is the idea that you can take a dataset of particular problems that are labelled by humans with correct results, and then feed them to a model which attempts to (by applying a particular algorithm and doing a bunch of math) predict the correct result for each problem, then look at the right answers, do more math to approximate how off the algoritm is by how wrong the predictions were, and then make adjustments to its algorithm to try and be less wrong on the next go around.
That making adjustments part is the learning.
The ‘how wrong its prediction was’ part is represented by a cost function (often interchangeably used with loss function), and each full go-around of predictions the model is trying to adjust its algorithm to be less and less wrong (ie. minimize the cost function). The entire process is called ’training’, and each time the model goes through all the data and makes a full set of predictions is called an ’epoch.’ So a simplified version of what the training might look like over several epochs looks like this:
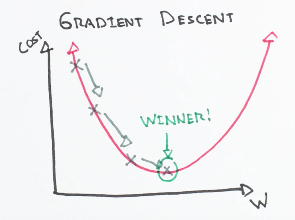
As the graph moves to the right, the model is progressing through the same training set of data and making predictions while seeing how wrong it’s predictions are, adjusting its algorithm, and trying again and again to minimize the cost function (the number of errors its making) so that the curve moves down.
This is a very, very simple explanation of stochastic gradient descent, where the ‘descending’ part refers to the line moving down as it minimizes how wrong its predictions are, and the ‘stochastic gradient’ part means complicated math that we don’t need to get into.
Overfitting
You may have noticed that the progress line starts going up at some point, meaning it’s starting to make more errors instead of less.
Again, I’m sure I don’t understand all the reasons and ways in which this can happen, but my simplified understanding is that when you try to learn to solve a parcticular problem by trying the exact same examples over and over, at some point you stop learning the general skill of solving that problem and start learning just how to best solve those specific examples - that’s called overfitting.
Like if you did the same 20 multiplication problems over and over, in the beginning you might start to learn generally how to multiply numbers, but by the end you’re just memorizing the right answers to the same 20 multiplication problems and not necessarily learning useful things about how you would solve new multiplication problems you haven’t seen before. You’re overfitting to the training set of data, which are the problems you keep trying over and over.
That’s bad, because the idea of learning is to learn generally how to solve the problem, not to get the solutions to the exact example problems you’re trying over and over.
In an amazing free online course I took on the basics of practical machine-learning called Fast AI (which I highly recommend for anyone with a bit of coding knowledge who wants to learning the basics of ML and train their own useful models), you’re taught to watch the results as you train your model through multiple epochs and stop just as you hit the bottom of the curve. Which makes sense, because after that the model starts making more and more errors and seems to be overfitting.
So double descent means you shouldn’t stop?
I thought so. I saw this graph that was shown in the Sutskever interview, and immediately thought that’s what they were talking about:
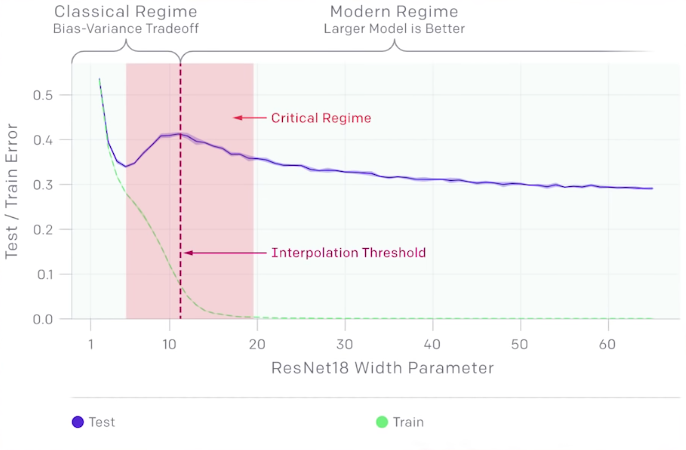
Turns out, not even close. Upon looking a little more closely at the graph, I noticed the x axis wasn’t number of training epochs like I had assumed (being familiar with watching for it from my Fast AI training), but instead the number of parameters that a model has.
What?
Basically, as I understand it parameters are the different variables you each a model to notice while it’s trying to solve a problem - like if you’re creating a model that classifies dogs, parameters might be their size, colour, shape, etc. Too few parameters, and the model is going to have trouble distinguishing between different dogs (like if you don’t have size as a variable, then you’d have trouble distinguishing between different breeds that are usually different sizes). Too many parameters, though, and you might start trying to classify based on very specific details that don’t actually relate to breed differences (like if you were watching for dogs that had bigger left ears than right - interesting, but I doubt that has anything to do with specific breeds).
So what that interview graph is showing is not how many errors are being made over a number of training epochs, but rather how many errors are being made according to how many parameters a model is paying attention to when trying to solve the problem.
That means that double descent isn’t about pushing through what Fast AI trained me to do in terms of stopping training at the epoch where loss seems to be about to turn up on the loss graph. Instead, it’s that when you’re deciding how many things your model should be paying attention to when solving the problem you’re training it solve, at some point when you’re increasing the number of variables it seems to make the model worse for awhile, but then as you keep increasing the number of parameters it will again start to make the model better again.
Super interesting, but not at all what I at first thought it was.
5 minutes versus 5 hours, but also some caution
When I realized my mistake, I spent the requisite amount of time feeling stupid/embarrassed, and then wanted to figure out if/how I was wrong. In the past, this would’ve involved a lot of googling and reading, unless I got lucky enough to find an article that explained exactly the mistake I had made.
Instead, I just asked ChatGPT.
Jaime Mor: so i thought double descent had to do with how many epochs you were training the data, but looking at graphs of it it seems to have more to do with the number of model parameters?
ChatGPT: You are correct. Double descent is primarily related to the number of model parameters rather than the number of epochs used to train the model. The phenomenon of double descent occurs when the number of model parameters exceeds the number of training examples, and increasing the complexity of the model beyond this point can lead to improved generalization performance, even beyond the point where it starts to overfit the training data. In contrast, the number of epochs used to train the model can impact the training dynamics and the point at which the model begins to overfit the training data. However, it is not directly related to the phenomenon of double descent. That being said, the number of epochs used to train the model can impact the point at which the double descent occurs, and early stopping based on the validation loss can be used to prevent overfitting and to find the optimal point at which to stop training.
Now, in fairness this is a bit cherry-picked - at first, after asking ChatGPT to explain double descent to me, ChatGPT seemed to miss and then reinforce the error I had made:
Jaime Mor: So in some deep learning courses they say to observe the epoch at which generalization error starts to increase, and stop there. Are those courses wrong or outdated, because what really needs to happen is to keep going and push through the increase to the second descent?
ChatGPT: The decision to stop training at the epoch where the generalization error starts to increase is not necessarily wrong or outdated, but it may not always be optimal. If the goal is to obtain a model that performs well on new, unseen data, then it is important to prevent the model from overfitting to the training data. Stopping training at the epoch where the generalization error starts to increase is one way to prevent overfitting and to obtain a model that generalizes well. However, it is also true that continuing to train beyond this point may result in a model that performs even better on new, unseen data, due to the phenomenon of double descent. The decision to continue training or to stop at the first descent depends on the specific problem, the amount of available data, and the computational resources available for training. In practice, it is often useful to monitor both the training and validation loss throughout the training process, and to use techniques such as early stopping or regularization to prevent overfitting. It may also be beneficial to explore different model architectures and hyperparameters to find the optimal balance between model complexity and generalization performance.
I thought maybe a more powerful model than the GPT-3.5-turbo I was chatting with might have caught my error, but GPT-4’s answer wasn’t much different.
I still don’t fully understand, but after chatting some more it seems to be because even though double descent has more to do with model complexity (number of parameters) than number of training epochs, the idea of ’early stopping’ (which I think is what Fast AI was training me to do) does interact with the double descent issue in the even more complex subject of ’epochwise double descent’.
Long story short
Long story short - ChatGPT helped me to expose myself to, and start grappling with, some complicated stuff way faster than if I had just gone googling. For a nerd like me, it’s really, really fun.